
알고리즘은 일반적으로 인풋의 크기에 따라 소요되는 시간이 달라진다. 보통 인풋 크기가 커질수록 알고리즘이 실행되는데 더 오래 걸린다.
인풋은 컴퓨터의 성능이나 프로그래밍 언어 등 환경적인 것들에 따라서 달라진다.
그래서 정해진 것이 점근표기법, 빅오(Big-O)표기법이다.
점근 표기법은 n이 엄청 큰 수라는 가정하에 사용된다. n이 별로 크지 않으면, 안 좋은 알고리즘을 써도 프로그램이 돌아가는데엔 문제가 없기 때문이다.
또한, 점근 표기법은 절대적인 시간이 아닌 성장성을 보기 때문에 예를들어 2n²+8n+34라는 시간이 든다고 가정해보자.
처음에는 2n² 이 8n+34 보다 그래프가 낮을 순 있지만 n이 커지다 보면 2n²이 압도적으로 값이 커지는 것을 알 수 있다. 그렇기에 더 영향력이 있는 2n² 만 보고 뒤에 8n+34는 무시해버린다.
1 O(1) --> 상수
2n + 20 O(n) --> n이 가장 큰영향을 미친다.
3n^2 O(n^2) --> n^2이 가장 큰영향을 미친다.
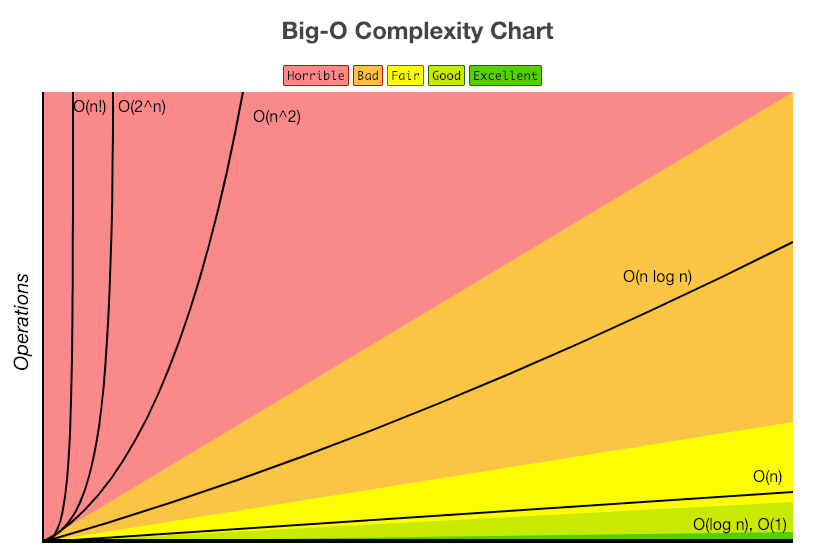
시간복잡도의 문제해결 단계를 나열하면 이와 같다.
O(1) – 상수 시간 : 문제를 해결하는데 오직 한 단계만 처리함.
O(log n) – 로그 시간 : 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬.
O(n) – 직선적 시간 : 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가짐.
O(n log n) : 문제를 해결하기 위한 단계의 수가 N*(log2N) 번만큼의 수행시간을 가진다. (선형로그형)
O(n^2) – 2차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱.
O(C^n) – 지수 시간 : 문제를 해결하기 위한 단계의 수는 주어진 상수값 C 의 n 제곱.
아래표는 실행시간이 빠른순으로 입력 N값에 따른 서로 다른 알고리즘의 시간복잡도이다.
| Complexity | 1 | 10 | 100 |
| O(1) | 1 | 1 | 1 |
| O(log N) | 0 | 2 | 5 |
| O(N) | 1 | 10 | 100 |
| O(N log N) | 0 | 20 | 461 |
| O(N^2) | 1 | 100 | 10000 |
| O(2^N) | 1 | 1024 | 1267650600228229401496703205376 |
| O(N!) | 1 | 3628800 | 화면에 표현할 수 없음! |
코드로 예를 들자면,
O(1) : 상수
아래 예제 처럼 입력에 관계없이 복잡도는 동일하게 유지된다.
def hello_world():
print("hello, world!")
O(N) : 선형
입력이 증가하면 처리 시간또는 메모리 사용이 선형적으로 증가한다.
def print_each(li):
for item in li:
print(item)
#선형탐색
def linear_search(element,some_list):
i = 0 # O(1)
n = len(some_list) # O(1)
while i < n : # O(1) x 반복횟수(n) => O(n)
if some_list[i] == element :
return i
i += 1
return -1 # O(1)
#O(1)+O(1)+O(n)+O(1)=O(n+3) => O(n)O(N^2) : Square
반복문이 두번 있는 케이스
def print_each_n_times(li):
for n in li:
for m in li:
print(n,m)
def print_triplets(my_list):
for i in range(len(my_list)):
for j in range(len(my_list)):
for k in range(len(my_list)):
print(my_list[i], my_list[j], my_list[k])O(log n)
주로 입력 크기에 따라 처리 시간이 증가하는 정렬알고리즘에서 많이 사용된다.
다음은 이진검색의 예이다.
def binary_search(element, some_list):
start_index = 0 #O(1)
end_index = len(some_list) -1 #O(1)
while start_indwx <= end_index: #최선의방법 : O(1) x 반복횟수(1), 최악의방법 :O(1) x 반복횟수(log n)
midpoint = (start_index + end_index) // 2
if some_list[midpoint] == element :
return midpoint
elif element < some_list[midpoint]:
end_index = midpoint - 1
else:
start_index = midpoint + 1
return None #O(1)
# O(1)+O(1)+O(log n)+O(1) = O(log n+3) => O(log n)은 과 이 중첩된 것이다. 같은 논리로, 은 과 이 겹쳐진 것이다.
# while문이 for문 안에 중첩
def print_powers_of_two_repeatedly(n):
for i in range(n): # 반복횟수: n에 비례
j = 1
while j < n: # 반복횟수: lg n에 비례
print(i, j)
j = j * 2
# for문이 while문 안에 중첩
def print_powers_of_two_repeatedly(n):
i = 1
while i < n: # 반복횟수: lg n에 비례
for j in range(n): # 반복횟수: n에 비례
print(i, j)
i = i * 2시간복잡도를 구하는 요령 (꿀팁)
각 문제의 시간복잡도 유형을 빨리 파악할 수 있도록 아래 예를 통해 빠르게 알아 볼수 있다.
- 하나의 루프를 사용하여 단일 요소 집합을 반복 하는 경우 : O (n)
- 컬렉션의 절반 이상 을 반복 하는 경우 : O (n / 2) -> O (n)
- 두 개의 다른 루프를 사용하여 두 개의 개별 콜렉션을 반복 할 경우 : O (n + m) -> O (n)
- 두 개의 중첩 루프를 사용하여 단일 컬렉션을 반복하는 경우 : O (n²)
- 두 개의 중첩 루프를 사용하여 두 개의 다른 콜렉션을 반복 할 경우 : O (n * m) -> O (n²)
- 컬렉션 정렬을 사용하는 경우 : O(n*log(n))
정렬 알고리즘 비교
| Sorting Algorithms | 공간 복잡도 | 시간 복잡도 | ||
| 최악 | 최선 | 평균 | 최악 | |
| Bubble Sort | O(1) | O(n) | O(n2) | O(n2) |
| Heapsort | O(1) | O(n log n) | O(n log n) | O(n log n) |
| Insertion Sort | O(1) | O(n) | O(n2) | O(n2) |
| Mergesort | O(n) | O(n log n) | O(n log n) | O(n log n) |
| Quicksort | O(log n) | O(n log n) | O(n log n) | O(n2) |
| Selection Sort | O(1) | O(n2) | O(n2) | O(n2) |
| Shell Sort | O(1) | O(n) | O(n log n2) | O(n log n2) |
| Smooth Sort | O(1) | O(n) | O(n log n) | O(n log n) |
자료구조 비교
| Data Structures | Average Case | Worst Case | ||||
| Search | Insert | Delete | Search | Insert | Delete | |
| Array | O(n) | N/A | N/A | O(n) | N/A | N/A |
| Sorted Array | O(log n) | O(n) | O(n) | O(log n) | O(n) | O(n) |
| Linked List | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Doubly Linked List | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Stack | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Hash table | O(1) | O(1) | O(1) | O(n) | O(n) | O(n) |
| Binary Search Tree | O(log n) | O(log n) | O(log n) | O(n) | O(n) | O(n) |
| B-Tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| Red-Black tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| AVL Tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
자료형 별 함수들의 시간복잡도
자료형 정리
자료형특징표현
| 리스트(List) | - 순서 O, 수정 가능(mutable) | list = [v1, v2, …] |
| 세트(Set) | - 순서 X, unique, mutable | set = {v1, v2, …} |
| 딕셔너리(Dictionary) | - 순서 X, 키(immutable), 값(mutable)이 맵핑 | dict = {k1:v1, k2:v2, …} |
리스트의 메소드 별 시간복잡도
| Operation | Example | Big-O | Notes |
| Index | l[i] | O(1) | 인덱스로 값 찾기 |
| Store | l[i] = val | O(1) | 인덱스로 데이터 저장 |
| Length | len(l) | O(1) | 리스트 길이 |
| Append | l.append(val) | O(1) | 리스트 뒤에 데이터 추가 |
| Pop | l.pop() | O(1) | 리스트 마지막 데이터 pop |
| Clear | l.clear() | O(1) | 빈 리스트로 만듬 |
| Slice | l[a:b] | O(b-a) | 슬라이싱 |
| Extend | l.extend(l2) | O(len(l2)) | 리스트 확장 |
| Construction | list(…) | O(len(…)) | 리스트 생성 |
| check ==, != | l1 == l2 | O(N) | |
| Insert | l[a:b] = … | O(N) | 데이터 삽입 |
| Delete | del l[i] | O(N) | 데이터 삭제 |
| Containment | x in/not in l | O(N) | x값 포함 여부 확인 |
| Copy | l.copy() | O(N) | 리스트 복제 |
| Remove | l.remove(val) | O(N) | 리스트에서 val값 제거 |
| Pop 2 | l.pop(i) | O(N) | i번째 인덱스 값 pop |
| Extreme value | min(l) / max(l) | O(N) | 전체 데이터를 체크해야함 |
| Reverse | l.reverse() | O(N) | 뒤집기 |
| Iteration | for v in l: | O(N) | |
| Sort | l.sort() | O(N log N) | 파이썬 기본 정렬 |
| Multiply | k*l | O(k N) |
세트의 메소드별 시간복잡도
| Operation | Example | Big-O | Notes |
| Add | s.add(val) | O(1) | 집합 요소 추가 |
| Containment | x in/not in s | O(1) | 포함 여부 확인 |
| Remove | s.remove(val) | O(1) | 요소 제거(없으면 에러) |
| Discard | s.discard(val) | O(1) | 요소 제거(없어도 에러x) |
| Pop | s.pop() | O(1) | 랜덤하게 하나 pop |
| Clear | s.clear() | O(1) | |
| Construction | set(…) | O(len(…)) | 길이만큼 |
| check ==, != | s != t | O(len(s)) | |
| <= or < | s <= t | O(len(s)) | 부분집합 여부 |
| Union | s, t | O(len(s)+len(t)) | 합집합 |
| Intersection | s & t | O(len(s)+len(t)) | 교집합 |
| Difference | s - t | O(len(s)+len(t)) | 차집합 |
| Symmetric Diff | s ^ t | O(len(s)+len(t)) | 여집합 |
| Iteration | for v in s: | O(N) | 전체 요소 순회 |
| Copy | s.copy() | O(N) |
딕셔너리의 메소드별 시간복잡도
| Operation | Example | Big-O | Notes |
| Store | d[k] = v | O(1) | 집합 요소 추가 |
| Length | len(d) | O(1) | |
| Delete | del d[k] | O(1) | 해당 key 제거 |
| get/setdefault | d.get(k) | O(1) | key에 따른 value 확인 |
| Pop | d.pop(k) | O(1) | pop |
| Pop item | d.popitem() | O(1) | 랜덤 데이터(key:value) pop |
| Clear | d.clear() | O(1) | |
| View | d.keys() | O(1) | key 전체 확인 |
| Values | d.values() | O(1) | value 전체 확인 |
| Construction | dict(…) | O(len(…)) | (key, value) tuple 갯수만큼 |
| Iteration | for k in d: | O(N) | 딕셔너리 전체 순회 |
출처-
https://blog.chulgil.me/algorithm/
https://duri1994.github.io/python/algorithm/python-time-complexity/
'알고리즘문제풀이' 카테고리의 다른 글
| [알고리즘/python] input() 과 sys.stdin.readline()의 차이 (0) | 2023.03.21 |
|---|---|
| [알고리즘/Python] 재귀함수와 팩토리얼 (0) | 2023.02.23 |
| [알고리즘/Python] BFS(너비우선탐색) (0) | 2023.01.18 |
| [알고리즘/Python] 깊이우선탐색 (DFS) (0) | 2023.01.18 |
| [알고리즘/Python] 그래프(Graph) (인접행렬,인접리스트) (0) | 2023.01.18 |





댓글